Sifat-sifat Turunan / Derivatif

Bila u = f(x), v=g(x), dan p=konstanta, maka:

1.
2.
3.
4.

Bagaimana kita tahu kalau 4 sifat itu benar? Atau, dari mana asal mula sifat itu? Hmm. Keep reading.. ^^
=========================================================================

BUKTI SIFAT-SIFAT TURUNAN

Sebelumnya, kita ingat-ingat kembali definisi turunan. Misalkan , maka:

Penambahan diakibatkan karena adanya penambahan .

Bila u = f(x), v=g(x), dan p=konstanta, maka bukti di bawah berlaku:

1.__	Andaikan . Penambahan berakibat penambahan dan , maka: Lalu, kita kurangkan kedua persamaan itu. __ Bagi keduanya dengan , lalu dekati ke nol. 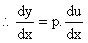(Terbukti)
2.__	Andaikan. Penambahan berakibat penambahan ,, dan , maka: Lalu, kita kurangkan dengan persamaan awalnya: __ Bagi kedua ruas dengan , lalu dekati ke nol. (Terbukti)
3.__	Andaikan. Penambahan berakibat penambahan ,, dan , maka: Kurangkan kedua persamaan akhir dan awal. __ Bagi kedua ruas dengan , lalu dekati ke nol. (Terbukti)
4.__	Andaikan . Penambahan berakibat penambahan ,, dan , maka: Kurangkan persamaan akhir dengan persamaan awal. __ Lalu, samakan penyebut. Bagi kedua ruas dengan , lalu dekati ke nol. (Terbukti)

=========================================================================
Empat sifat itu dapat dibuktikan dengan proses yang sama. Coba perhatikan.! Mudah bukan? Logika penyelesaiannya sebetulnya menggunakan proses ini: , tapi tidak dilakukan secara langsung, tapi secara bertahap.